
Mathematicians discover the ‘Einstein tile”, a shape that can tile a wall perfectly without creating a repeating pattern. Here’s everything you need to know.
What is the Einstein tile?
For long Mathematicians have been wondering about the existence of an “Einstein tile.” It is a shape that can singularly be used for creating a non-repeating or aperiodic pattern on a large plane. Here, ‘Einstein’ is a play on ein stein, the German word meaning one stone. David Smith, Craig S. Kaplan, Chaim Goodman-Strauss, and Joseph Samuel Myers’ new 13-sided shape solves a problem that has puzzled researchers for decades.
A set of prototiles are called aperiodic if their copies create patterns without repeating. Mathematician Hao Wang in 1961 suspected such a tile was impossible. However, Robert Berger later disputed this by finding a set of 104 tiles. Nobel prize-winning physicist Roger Penrose in the 1970s found a set of two tiles that can be arranged to form a non-repeating pattern. However, since then researchers have been in the search of a single holy grail of aperiodic tiling. Mathematicians call this the Einstein problem of geometry as it stumped them for decades.
Einstein tile: More on the discovery
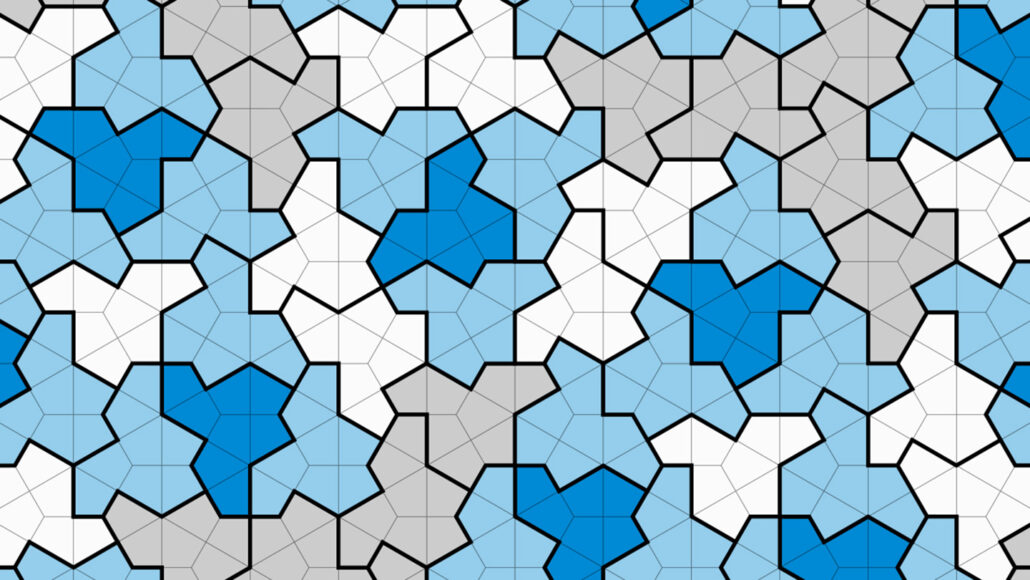
The 13-sided einstein tile named “the hat” presents a deceptive but simple solution. It comprises eight copies of a 60°–90°–120°–90° kite. When placed edge to edge, they help in generalizing an infinite set with the aperiodic property. It also retains the qualities when grouped with various lengths of sides. Moreover, David Smith, an amateur mathematician, and hobbyist is credited with discovering the shape. When asked about the discovery, Smith stated, “I’m always messing about and experimenting with shapes.” Smith worked with a mathematician and two computer scientists to develop the poofs needed.
“You’re literally looking for like a one-in-a-million thing. You filter out the 999,999 of the boring ones, then you’ve got something that’s weird, and then that’s worth further exploration,” stated Goodman-Strauss. “And then by hand, you start examining them and try to understand them and start to pull out the structure. That’s where a computer would be worthless as a human had to be involved in constructing proof that a human could understand,” he added. The discovery can help chemists and physicists understand the behavior and structure of quasicrystals. Additionally, this will also be a springboard for creative art.
